Finding the Value of C for Equal Areas in Calculus Puzzles
Written on
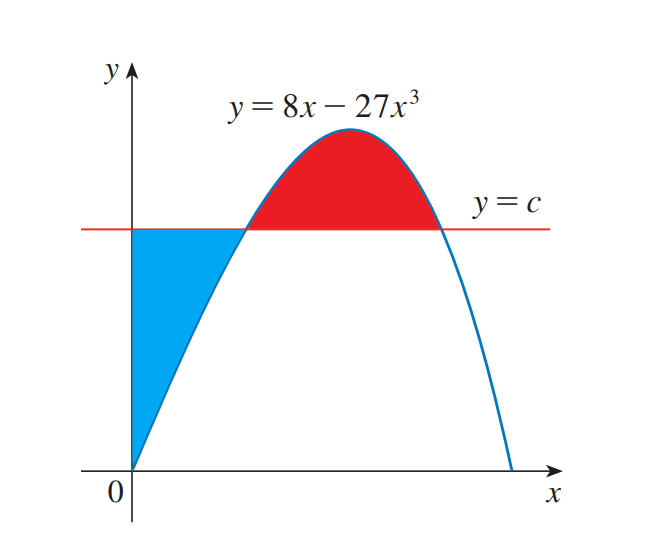
Understanding the Puzzle
Calculus offers an engaging way to challenge our comprehension. In this puzzle, we examine a horizontal line defined by y = c that intersects with the curve represented by y = 8x - 27x³. The intersection points will influence the areas of the regions colored red and blue.
Can you determine the value of c that equalizes the two areas? I encourage you to pause and attempt the problem using pen and paper. When you're ready, proceed to the solution!
Solution Approach
To start, let a and b represent the x-coordinates where the line meets the curve. Since both points lie on the line y = c, their y-coordinates are simply c. Thus, we have the points (a, c) and (b, c) as depicted.
Our objective is to ensure that the area R1 is equal to the area R2.
Calculating Area R1
To find the integral for R1, we consider the rectangle formed from x = 0 to x = a. The blue area, R1, can be calculated by subtracting the area of the yellow region from the total rectangle.
Mathematically, we can express this as follows:
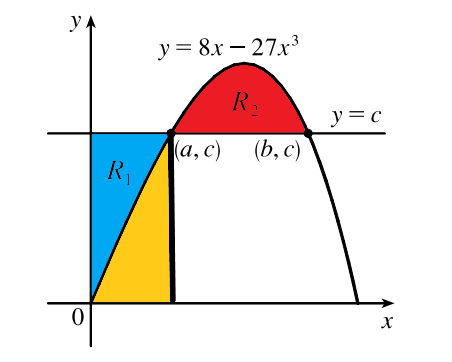
Area R2 Calculation
Similarly, we can determine the integral for R2 by examining the red region. To find R2's area, we subtract the yellow rectangle from the integral of the curve across the specified interval.
Mathematically, we get:
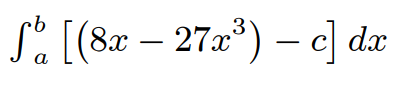
Mathematical Evaluation
Using the reverse power rule, we can evaluate the integrals and substitute the boundaries to derive an equation.
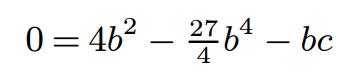
The challenge lies in expressing c in terms of b. Notice the point (b, c) on the graph, which lies on the curve y = 8x - 27x³. This gives us the equation:

Substituting and Solving
By substituting this expression into our equation, we can then factor it to find:
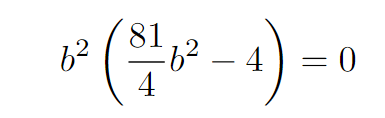
Given that b must be greater than zero, we can conclude that 81/4b² - 4 = 0, leading to the result b = 4/9.
To find the corresponding value of c that equates the two areas, we substitute b = 4/9 back into our equation:

Conclusion
And there you have it! How fascinating was that? What were your thoughts during this exercise? Please share your reflections in the comments; I'm eager to hear from you!
Additional Resources
For more intriguing math puzzles, consider checking out these curated collections on Medium!
Math Puzzles
The best math puzzles on Medium covering Algebra, Geometry, Calculus, Number Theory, and much more!
Thank you for reading! If you found this article insightful, please give it a clap!
