Chapter 1: Introduction to the Problem

What is the function that meets the differential equation presented and the additional condition? This is a typical calculus question found in the Practice 18.01 Advanced Placement Exam — Part I from the Massachusetts Institute of Technology. A previous problem was discussed here.

This question assesses our grasp of the separation of variables, a fundamental method in ordinary differential equations. A helpful guideline to remember is to arrange all x’s on one side and all y’s on the other.

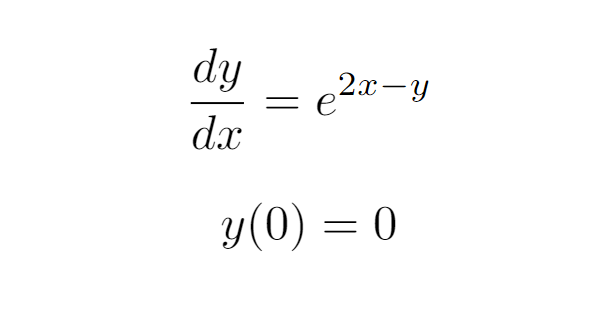
By doing this, we ensure that each part can be integrated with respect to its respective variable.

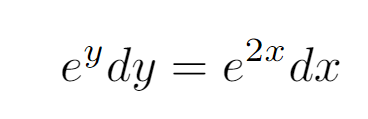
Upon performing the integration, we can combine the constants from both integrals, c1 and c2, into a single constant, C.

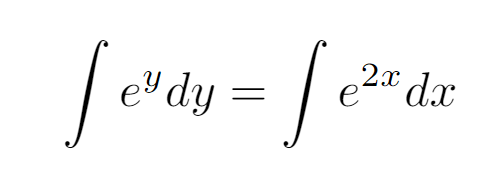
As for the additional condition y(0) = 0, it indicates that when x = 0, y must also equal 0. This piece of information is vital as it assists us in determining the value of C.

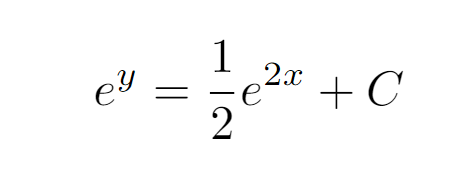
Now that we have established the constant C, we can express the function y in terms of x. By applying the properties of logarithms and exponentials, we arrive at the final solution.

And there you have it—our solution! How remarkable is that? What was your thought process on this problem? Feel free to share your insights in the comments; I’m eager to hear from you!

Chapter 2: Exploring Further

Math Puzzles

Check out the most intriguing math puzzles on Medium, covering topics like Algebra, Geometry, Calculus, and Number Theory. Share this with your friends!

Thank you for your time! If you found this article useful, please consider giving it a clap.

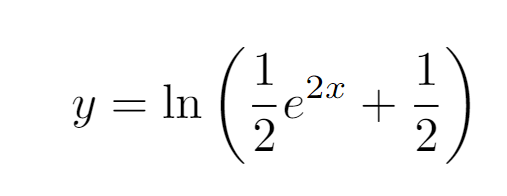
If you wish to support my work, feel free to buy me a coffee! Your generosity means the world to me and helps sustain my writing journey.

With appreciation, Bella