Section 1.1: Analyzing the Problem

Upon first glance, we can simplify one of the terms on the left-hand side by both adding and subtracting it. This leads us to two new equations:

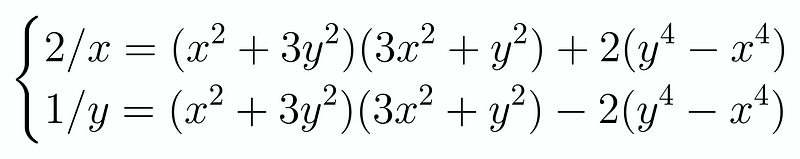
Naturally, we proceed to expand this to see if it produces a more manageable form. The result is as follows:

We observe that the upper and lower parts of our expression are closely related, merely rearranging the same coefficients. Let's continue to multiply out the left side to obtain:

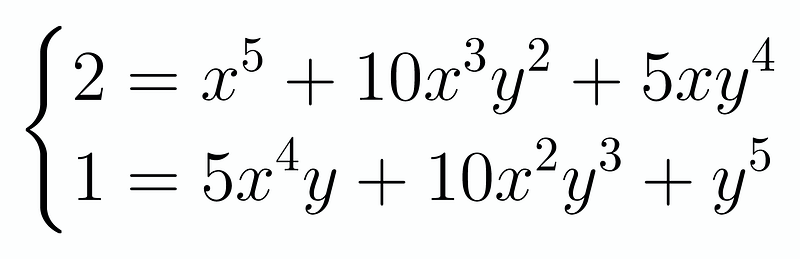
This expression holds true as long as neither x nor y equals 0. It appears that every term is distinct yet bears the same coefficients. Initially, this may seem problematic, but we recognize that these coefficients correspond precisely to the binomial coefficients. Hence, we can once again add and subtract these terms, leading to the following expression:

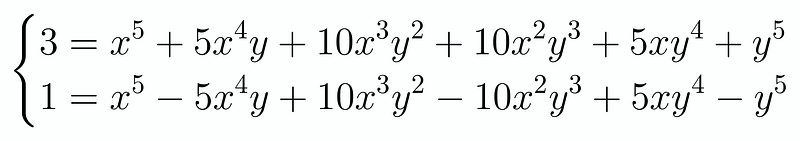
Consequently, we arrive at:

This expression is much more straightforward! Given that 5 is an odd number and we are only interested in real solutions, we can now take the 5th root of both sides, resulting in a pair of linear equations:

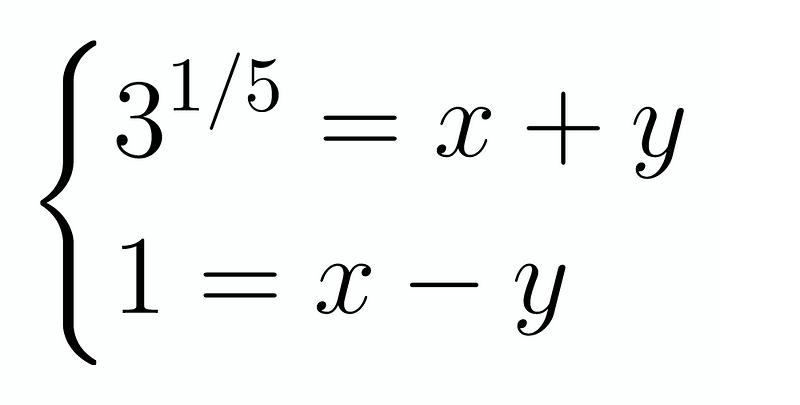
This makes it easy to solve. By adding and subtracting the equations one final time, we arrive at:

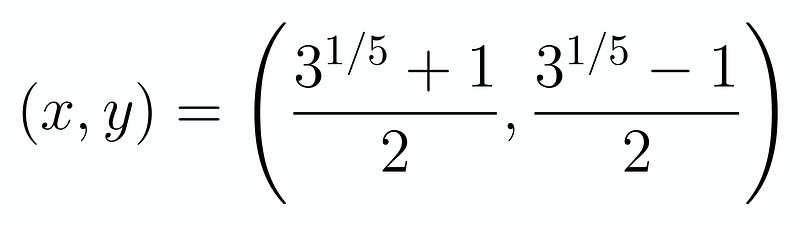
as our sole real solution. To verify, we can utilize online graphing software:

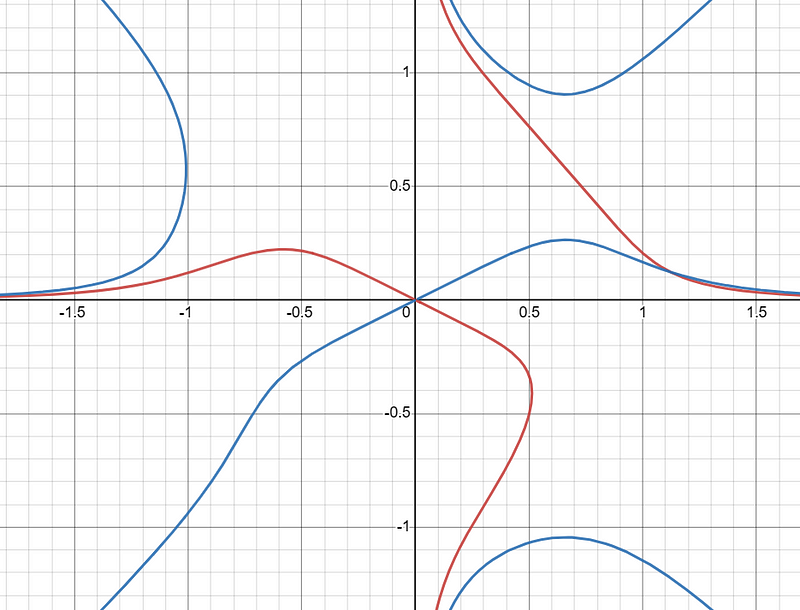
This indeed confirms our solution (note that the equations do not intersect at 0, instead behaving asymptotically, getting increasingly close without crossing at the axis).

Chapter 2: Exploring Functional Equations

In this chapter, we will explore a beautiful trick for solving functional equations, specifically referencing Putnam 1988 problem A5.

This video provides insights into elegant methods used in tackling functional equations, showcasing techniques that can be applied to various problems.

Chapter 3: Number Theory and Putnam Challenges

Next, we will tackle a seemingly simple number theory problem from Putnam 1988.

This video challenges viewers to solve an easy number theory problem, highlighting the importance of problem-solving skills in the Putnam competition.