Chapter 1: Introduction to Faraday’s Law

Faraday’s Law holds significant importance in the realm of physics. It asserts that a varying magnetic flux generates an electric field, which subsequently induces a change in electric potential across a closed circuit—commonly referred to as electromotive force (EMF). The mathematical representation of this concept can be summarized as follows.

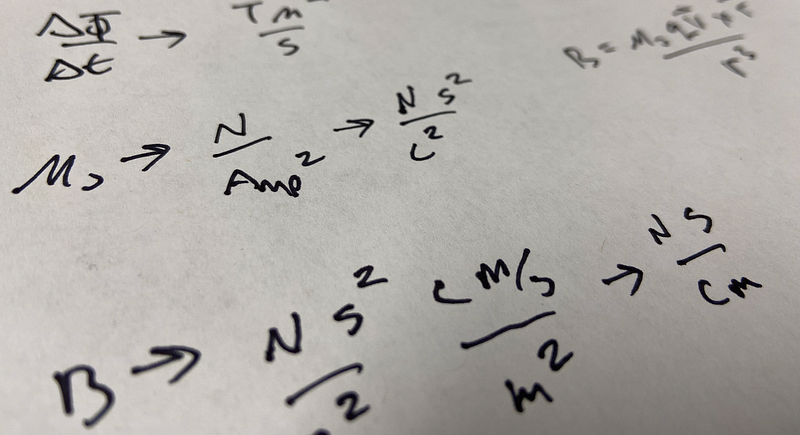
However, one might wonder about the role of the negative sign in the equation. Personally, I find the negative sign somewhat unnecessary here. While it plays a part in the integral formulation of Faraday’s Law, in this context, it seems irrelevant. Moreover, it lacks specific units. The variable "N," representing the number of loops, is understandable but also unitless.

Now, focusing on the left side of the equation, we encounter the electromotive force, which is measured in Volts. But what about the right side? While time is expressed in seconds, magnetic flux requires further explanation.

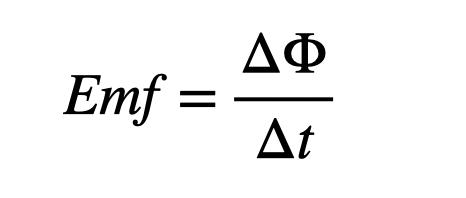
This expression represents magnetic flux for a constant magnetic field over a flat surface. Ultimately, the units are what matter. The cosine function presents no complications, as it is simply a ratio derived from a triangle's sides. Regarding area, when using standard units, we measure it in square meters (m²).

The magnetic field is a bit trickier. It's quantified in Teslas, but that might not provide much clarity. The crucial step is to establish a relationship that includes the magnetic field alongside known quantities. My initial thought was to consider the magnetic field resulting from a moving charge.

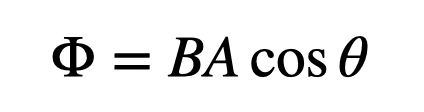
I have the units for everything here, except for one constant. Rather than trying to ascertain that unit, let's explore another equation. No, looking up the unit would be cutting corners, and I want to avoid that.

Next, I considered the force exerted on a moving charge within a magnetic field.

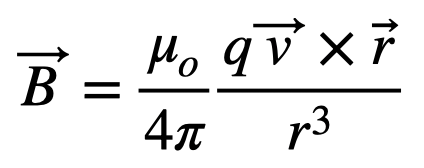
This approach is more effective, as there are no unknown constants. The vector components are irrelevant here. If I simply outline the units, I arrive at the following.

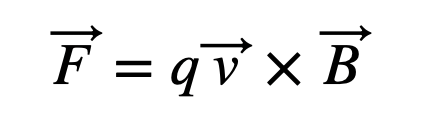
Although it might not be a conventional equation—perhaps it is, I’ll need to contemplate that further—it's still valid to use this and "solve" for T.

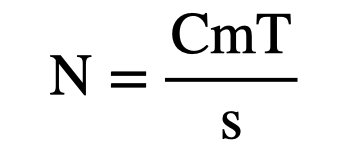
Now, I can compile all of this information to explore the right-hand side of the equation, relating to the change in magnetic flux over time.

It's important to note that I use the arrow to transition from an expression to units, as I want to avoid equating them directly. Still, I'm approaching the Volts unit found on the left side of the equation.

What if we use the work definition? I will simplify the integral definition and assume a constant force applied in a straight line.

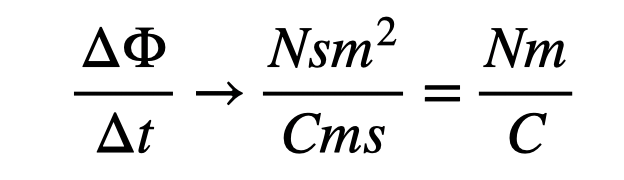
The unit for work is Joules, where 1 Joule equals 1 Newton multiplied by meters. Thus, Nm = J. At last, I can apply the definition of the change in electric potential.

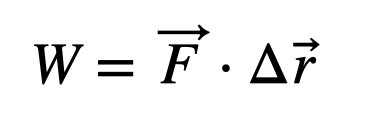
This gives us Joules per Coulomb, equating to a volt. And there we have it—problem solved.

It's worth mentioning that just because both sides of an equation bear the same units, it doesn't automatically validate the equation. If the units don’t align, however, that indicates an error.

This process is known as dimensional analysis.

This video, titled "Unit Check: Faraday's Law," provides an overview of the units involved in Faraday's Law and their significance in practical applications.

Chapter 2: Further Exploration of Electromagnetic Principles

In continuation of our exploration, we will delve deeper into the topics of electromagnetic induction, including Faraday's and Lenz's laws.

The second video, "Review of Unit on Electromagnetic Induction, Faraday's Law, and Lenz's Law (part II)," offers a comprehensive review of these principles and their interconnections.