# Understanding the Beta Function: Key Insights and Applications
Written on
Chapter 1: Introduction to the Beta Function
Among the various special functions, the Beta function tends to be the least recognized. While its usage is primarily noted in statistics and probability theory, this does not diminish its significance. The Beta function often appears in calculations, only to vanish shortly after. Below, you'll find a comprehensive overview of everything essential to know about the Beta function.
This article serves as the second part of a mini-series focused on special functions. For additional articles on related topics, please refer to the accompanying list.
Section 1.1: Recognizing the Beta Function
The main challenge with the Beta function lies in identifying it, as it can manifest in several distinct forms. The standard definition is represented by the integral:
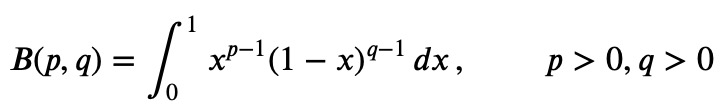
This resemblance to binomial distributions is likely the origin of its name, the Beta function.
To derive the trigonometric expression of the Beta function, one can employ the substitutions ( x = t^2 ) and ( t = sin(theta) ), leading to:
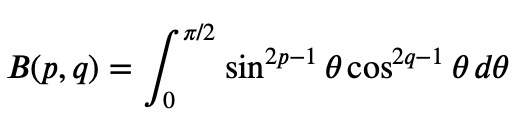
A third form can be obtained by substituting ( x = frac{t}{1+t} ) into the original definition:
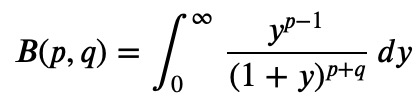
Memorizing these various representations of the Beta function is advantageous, as it allows for the transformation of complex integrals into a Beta function format, making them easier to solve.
Section 1.2: Properties of the Beta Function
One notable property of the Beta function is its symmetry:
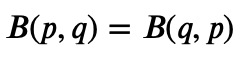
When encountering the Beta function, it’s often beneficial to convert an integral into a Beta function form. Why? Because this transformation allows for its replacement with Gamma functions, which are simpler to work with. The following relationship is crucial for this purpose:
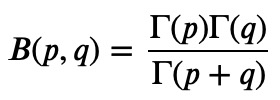
This relationship is worth committing to memory. A straightforward proof can be derived by writing out the Gamma function's definition and substituting ( x = t^2 ):
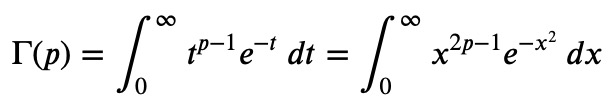
Next, apply the same method for ( Gamma(x) ) and document the product:
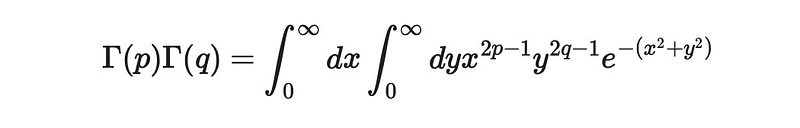
It’s noteworthy that I’ve opted for a notation typically used by physicists, placing the differentials at the start of the integral for clarity regarding the respective integration variable’s boundaries.
When considering ( x ) and ( y ) as Cartesian coordinates, a transformation to polar coordinates can be made:

Here, the upper limit of the ( y ) integral is ( frac{pi}{2} ) instead of ( 2pi ), as we’re only integrating over the first quadrant where ( x, y geq 0 ). The ( y ) integral corresponds to a Gamma function, specifically ( Gamma(x+y) ), while the ( x ) integral represents a Beta function, completing the proof.
Chapter 2: Application Example
For instance, consider the integral:

This integral is closely related to the first form of the Beta function. By making the substitution ( t^2 = u ):
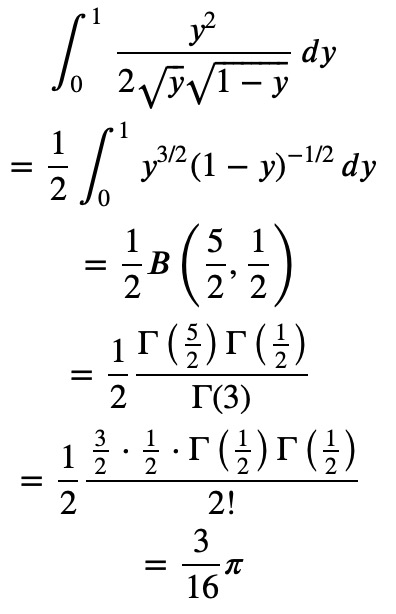
In this context, we’ve utilized certain properties of the Gamma function. Remember how the Gamma function is defined:
Cheat Sheet for Reference
For your convenience, here’s a summary of the key points regarding the Beta function:
