Exploring Inelastic Collisions: A Problematic Encounter
Written on
Chapter 1: Introduction to Inelastic Collisions
In this exploration of inelastic collisions, we analyze a scenario set in the vastness of space. Picture yourself on a spacewalk, floating outside a spaceship that's gliding through the void. You have deployed a reference probe that remains perfectly still in relation to the vessel, equipped with advanced laser velocity measurement tools. Suddenly, a meteoroid, traveling at 4.0 m/s, collides with the ship and rebounds in the opposite direction at 2.0 m/s.
After capturing the meteoroid, you place it into the ship and weigh it using an inertial mass meter, revealing it to have a mass of 1.0 kg. The ship itself has a mass of 20,000 kg when unoccupied. Due to this impact, the spaceship begins to move relative to the probe in the same direction that the meteoroid was initially headed.
The question arises: what velocity will the probe record for the ship after the collision? The answer should be expressed in millimeters per second (mm/s). — (Gibiliseo 2007, p. 31)
Attempted Solution
To tackle this physics problem, I began by sketching out the scenario. Figure 1 illustrates my conceptualization of the situation:
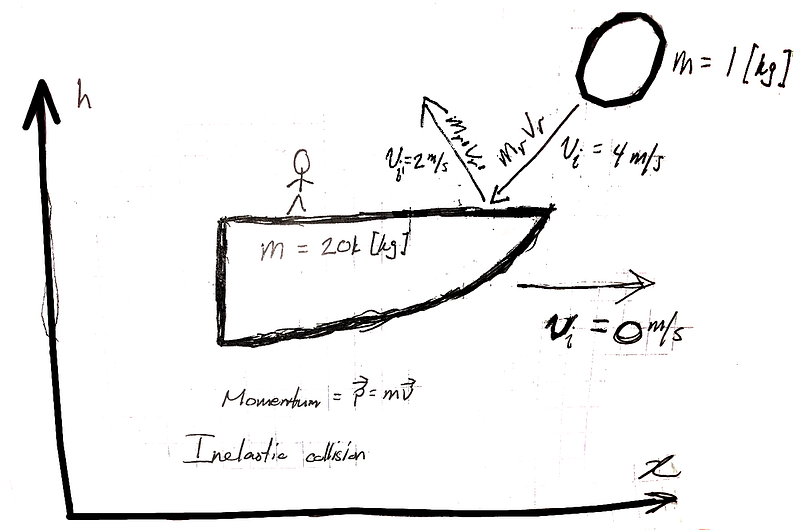
Figure 1
As noted, I made observations in the lower section of my sketch, identifying this as an inelastic collision case. Subsequently, I constructed a general depiction of what an inelastic collision might entail, represented in Figure 2:
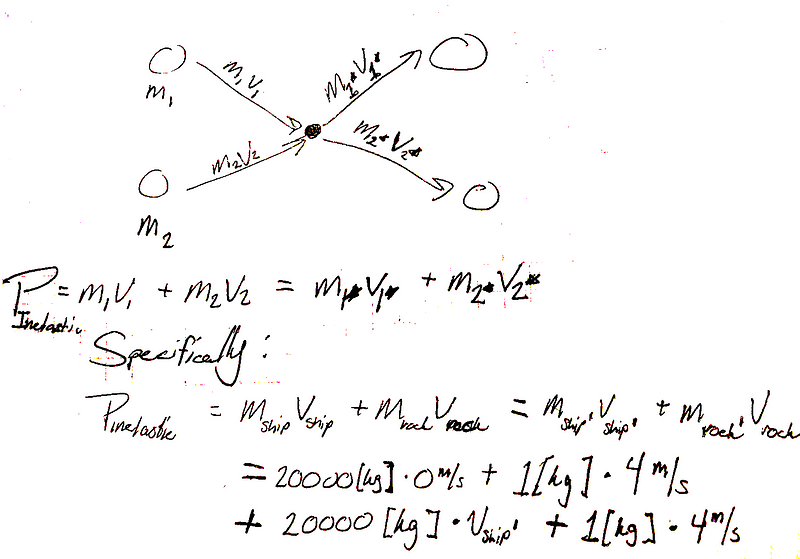
Figure 2 (after Gibiliseo 2007, p. 31)
Figure 2 provides a broader overview of collisions, whether they are perfectly elastic or inelastic, alongside a formal analysis of inelastic collisions pertinent to this specific problem.
Equation 2.1 represents the algebra utilized to derive the solution in meters per second:
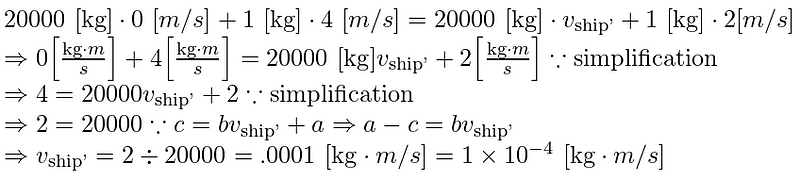
Eq. 2.1
It is important to note that the second simplification eliminates units to prevent confusion; I will reintroduce them once the problem is solved. The final answer must be provided in millimeters per second [mm/s], which I calculated using unit conversion in Equation 2.2:
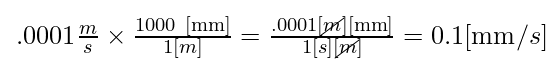
Eq. 2.2
Initially, I arrived at an answer of 0.1 [mm/s], but it has become evident that this is incorrect. The accurate result is 0.3 [mm/s], prompting me to investigate where I went wrong in my calculations.
Trying Again
Given that the correct outcome is 0.3 [mm/s], I must have miscalculated during my initial attempt. Perhaps I mistakenly interpreted the nature of the collision. I then re-evaluated the problem using a different approach, considering a partially elastic collision:
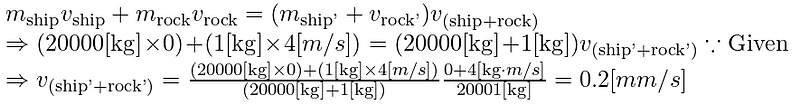
Eq. 3.1
The result of two-tenths of a millimeter per second still deviates from the correct answer.
End Matter
Ultimately, the verified answer remains at 0.3 [mm/s], leaving me puzzled about where my understanding faltered. It seems I may have incorrectly classified this as a collision problem. If it is indeed a collision scenario, then my interpretation of the provided information and my free-body diagram—both figuratively and literally—might have been flawed. I look forward to revisiting this problem in the future.
References
Gibiliseo, S. (2007). Advanced Physics Demystified [Paperback]. McGraw-Hill Education.
Chapter 2: Video Explanations of Inelastic Collisions
This video titled "How to Solve an Inelastic Collision Problem" offers a detailed breakdown of the steps and strategies for solving inelastic collision problems, providing a valuable visual aid to enhance understanding.
In the video "Perfectly Inelastic Collision: Conservation of Momentum and Impulse," viewers will learn about the principles of momentum conservation and impulse in the context of perfectly inelastic collisions, further solidifying the concepts discussed.