Chapter 1: Understanding Squares

In mathematics, a square is defined as a number multiplied by itself; for instance, 3 multiplied by 3 equals 3². While this may be straightforward for many, the concept can become daunting when dealing with variables like x² and quadratic equations, causing interest to wane.

However, a more intuitive understanding of squares can be drawn from geometry, specifically the classic shape of a square. This article aims to illustrate how seemingly tedious algebraic operations involving squares can be approached through visual methods, making them more engaging. We will begin with basic concepts and gradually explore more advanced ideas, equipping you with the tools to delve deeper on your own.

What Are Squares?

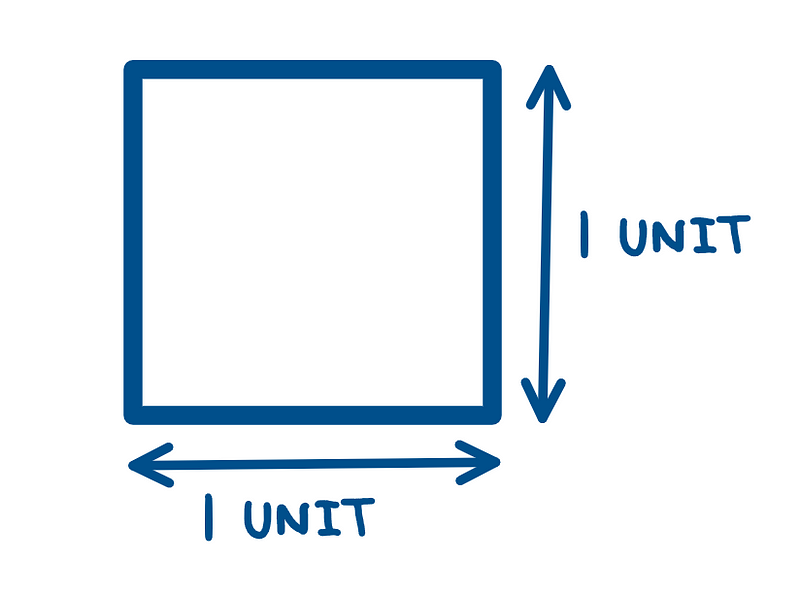
Let’s start with a basic square, which we will define as having a side length of 1 unit (this could be in centimeters, millimeters, etc.). We will refer to this as a unit square, as it represents the square of the integer 1.

Now, consider the following question: “What is the minimum number of unit squares required to create a larger square?”

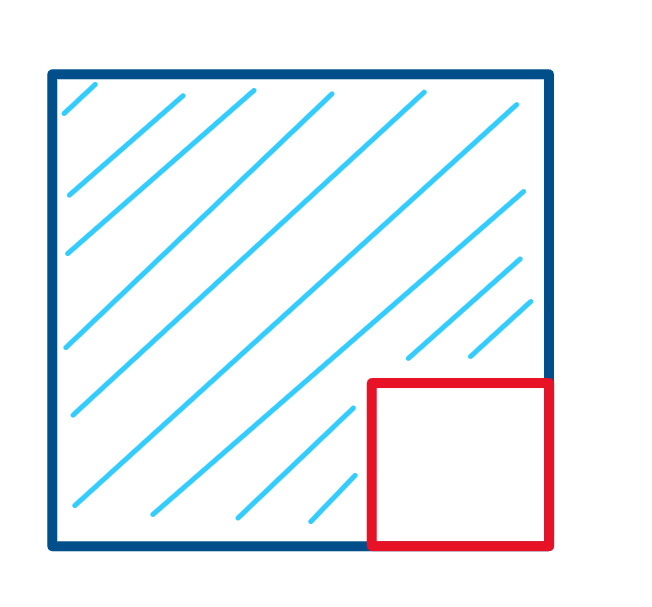
The answer is that four unit squares combine to form a 2x2 square, commonly referred to as the square of the integer 2 (or 2-squared).

Continuing this pattern, the next larger square is 3-squared, which consists of nine unit squares, and thereafter, 4-squared comprises sixteen unit squares. This visual method can be applied to comprehend squares of larger integers as well.

Now that we have a foundation for understanding integer squares through geometry, let’s explore more complex applications.

Difference of Squares

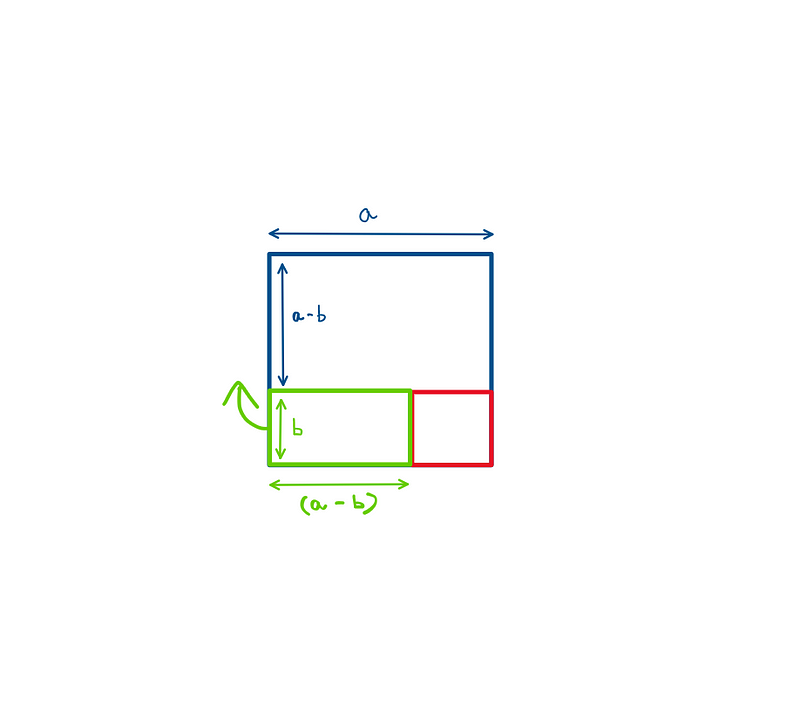
Imagine two squares: a larger one with a side length of ‘a’ and a smaller one with a side length of ‘b’.

To find the difference in their areas, we can visualize this scenario in real-life applications, such as tiling or assembling wooden furniture. One method involves overlaying the smaller square onto the larger square and calculating the area of the shaded region.

Alternatively, there’s a simpler approach: remove a rectangle with the height of the smaller square and reposition it alongside the remaining area of the larger square. This creates a rectangle with a length of (a+b) and a height of (a-b). By calculating the area of this rectangle, we can determine the difference of the squares.

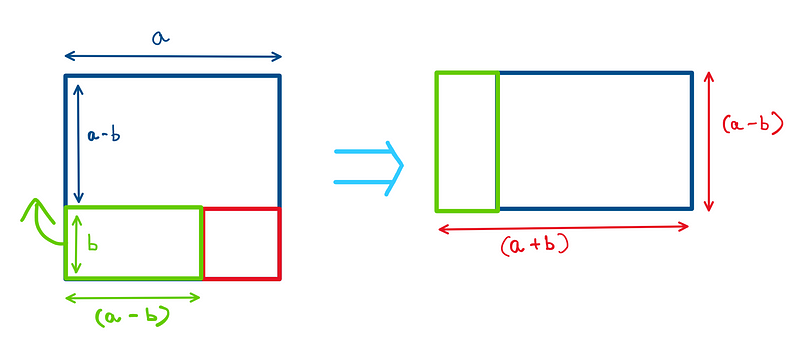
This method reduces the complexity from two multiplications to one, simplifying the problem-solving process. The algebraic equivalent of this identity can be expressed as follows:

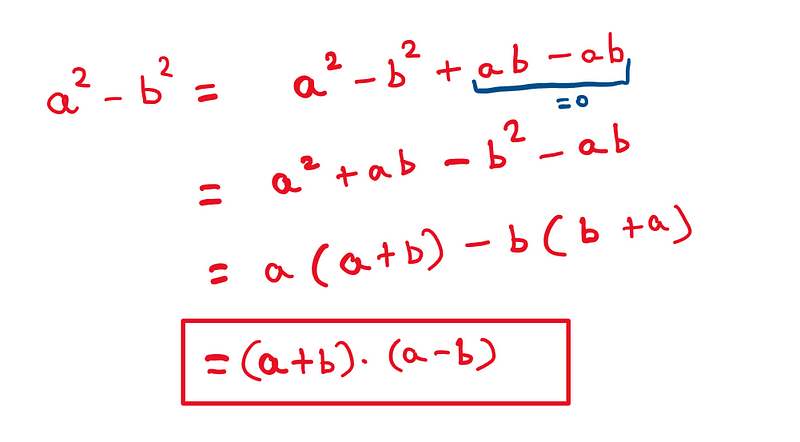
Let’s explore another application of this visual approach.

Proving Any Odd Number as a Difference of Successive Squares

A fundamental theorem in number theory states that any odd number can be expressed as the difference between two successive squares. Before delving into the formula, let’s visualize this concept.

Consider the odd number 5. We can represent it using five unit squares arranged in a line, and then manipulate them into an inverted L-shape:

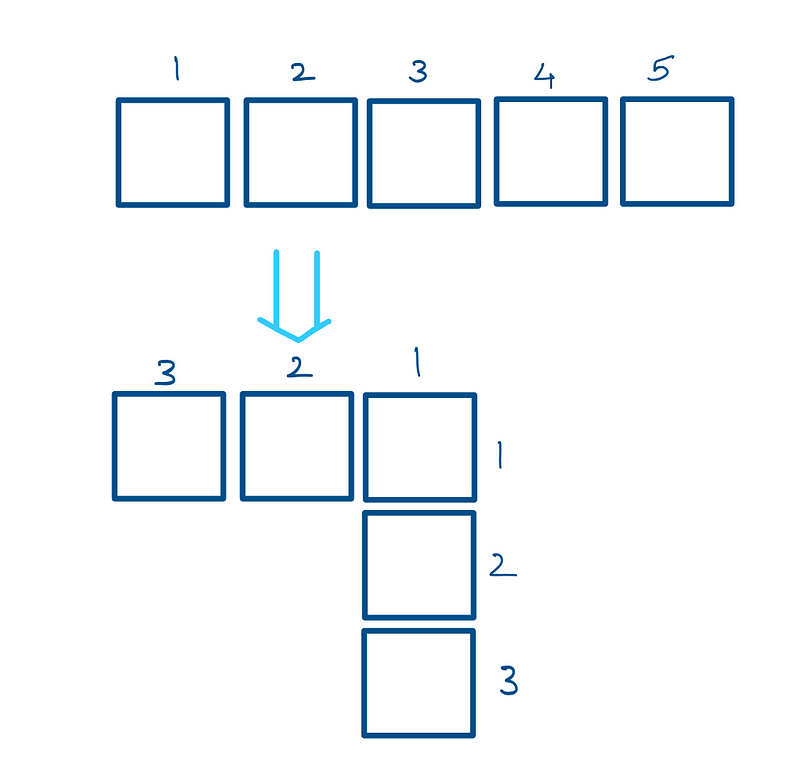
Next, we fill in the empty spaces on the lower left with additional unit squares, resulting in four more squares.

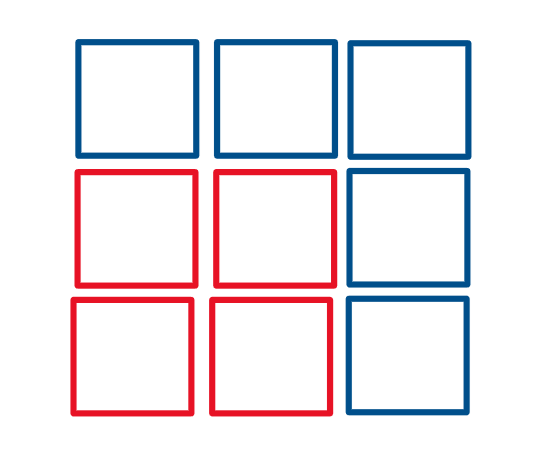
Upon closer examination, we have two squares: a larger 3x3 square and a smaller 2x2 square. Subtracting their areas yields: 3² - 2² = 9 - 4 = 5, confirming our initial odd number.

By experimenting with larger numbers, you will find that any odd number K can be expressed as k = (n+1)² - n², where k = (2n + 1). The algebraic expression of this is as follows:

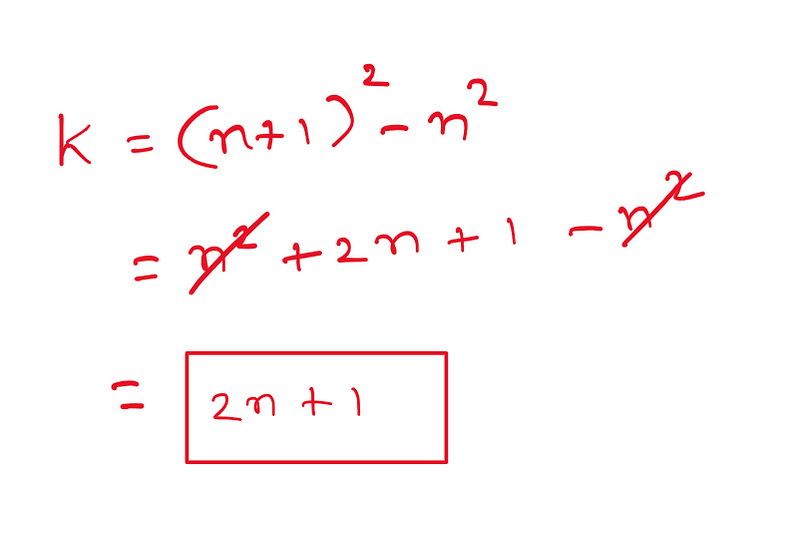
Exploring Higher Dimensions

I have illustrated several examples of how visual methods can facilitate problem-solving and foster a deeper understanding of mathematics. Consider this a starting point; the more creativity you apply, the more enjoyable and effortless your mathematical explorations will become.

To conclude, let’s consider how this visual approach can be expanded into higher dimensions. Recall how we calculated the area difference between two squares visually? It requires minimal additional thought to extend this to the volume difference in cubes. What applications could arise from such a process? And what about dimensions beyond that? The fourth-dimensional counterpart of a cube is known as a tesseract.

The above image shows a projected rotation of a tesseract along two planes. Ponder its potential uses and how we could adapt our visual methods to navigate higher dimensions.

I hope you found this article both intriguing and informative. If you’d like to support my work as an author, please consider clapping, following, and subscribing.

Further reading that might pique your interest: "How Imagination Enhances Mental Math Skills" and "Is It Time to Redefine Traditional Education?"

Video Resources

Classroom Activity: Square Roots Discover engaging classroom activities that help students understand square roots through fun and interactive methods.

Making Math Review a High-Energy Game Learn how to turn math reviews into exciting games that keep students energized and engaged.