Understanding the Wilcoxon Test in R: A Non-Parametric Approach
Written on
Introduction to Non-Parametric Testing
In an earlier article, we explored how to assess differences between two groups utilizing the Student’s t-test. This test is contingent upon the assumption that the data follows a normal distribution, particularly in cases involving small sample sizes. This article will guide you through the process of comparing two groups when this normality assumption is not upheld, specifically through the use of the Wilcoxon test.
The Wilcoxon test is classified as a non-parametric test, which means it doesn’t rely on the data conforming to a specific parametric family of probability distributions. Non-parametric tests serve the same purpose as their parametric counterparts but offer the benefit of not requiring the assumption of normality. For instance, the Student’s t-test is only applicable if the data is Gaussian or if the sample size is sufficiently large (typically n ≥ 30). Consequently, non-parametric tests should be employed in other situations.
You might wonder why non-parametric tests aren't always the preferred choice. The answer lies in their generally lower power compared to parametric tests when the normality assumption is satisfied. In simpler terms, if the data follows a normal distribution, using a non-parametric test may lead to a lesser chance of rejecting the null hypothesis when it is indeed false. Therefore, it is advisable to use the parametric version of a statistical test when the underlying assumptions are validated.
In the subsequent sections, we will delve into the two scenarios applicable to the Wilcoxon test and demonstrate how to execute them in R through practical examples.
Two Distinct Scenarios
Similar to the Student’s t-test, the Wilcoxon test is utilized to evaluate whether two groups exhibit significant differences. The groups being compared can either be:
- Independent
- Paired (dependent)
The Wilcoxon test encompasses two variations:
- The Mann-Whitney-Wilcoxon test (often referred to as the Wilcoxon rank sum test) is employed when the samples are independent, serving as the non-parametric counterpart to the Student’s t-test for independent samples.
- The Wilcoxon signed-rank test (sometimes simply called the Wilcoxon test for paired samples) is used when the samples are paired or dependent, acting as the non-parametric equivalent to the Student’s t-test for paired samples.
Fortunately, both tests can be conducted in R using the same function: wilcox.test(). The following sections will elaborate on each of these scenarios.
Independent Samples
For the Wilcoxon test with independent samples, let’s consider an example where we aim to determine if there is a difference in exam grades between female and male students. We collected grades from 24 students (12 girls and 12 boys):
dat <- data.frame(
Sex = as.factor(c(rep("Girl", 12), rep("Boy", 12))),
Grade = c(19, 18, 9, 17, 8, 7, 16, 19, 20, 9, 11, 18,
16, 5, 15, 2, 14, 15, 4, 7, 15, 6, 7, 14)
)
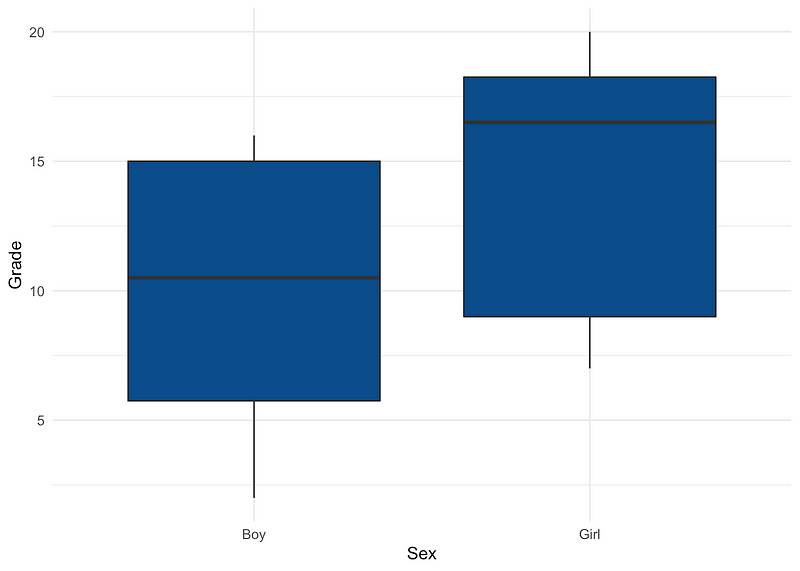
Here are the grade distributions by gender (using {ggplot2}):
library(ggplot2)
ggplot(dat) +
aes(x = Sex, y = Grade) +
geom_boxplot(fill = "#0c4c8a") +
theme_minimal()
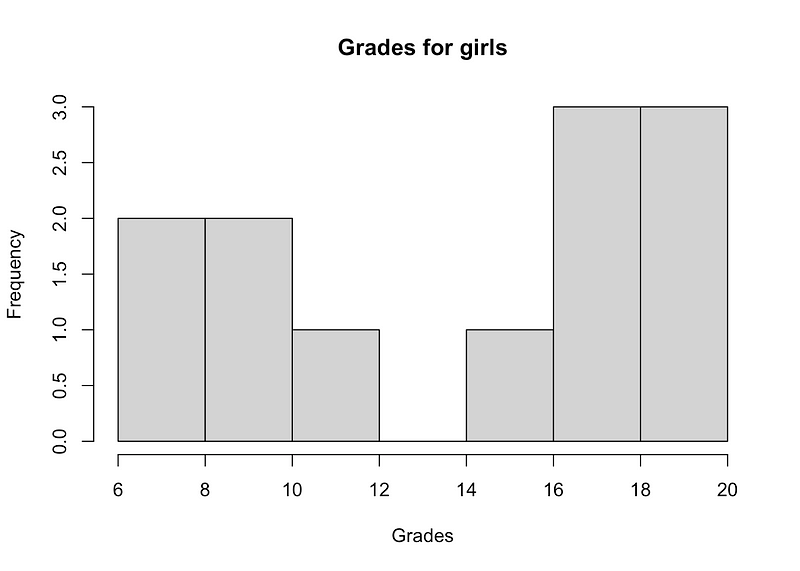
Next, we’ll assess whether the two samples adhere to a normal distribution via a histogram and the Shapiro-Wilk test:
hist(subset(dat, Sex == "Girl")$Grade, main = "Grades for girls", xlab = "Grades")
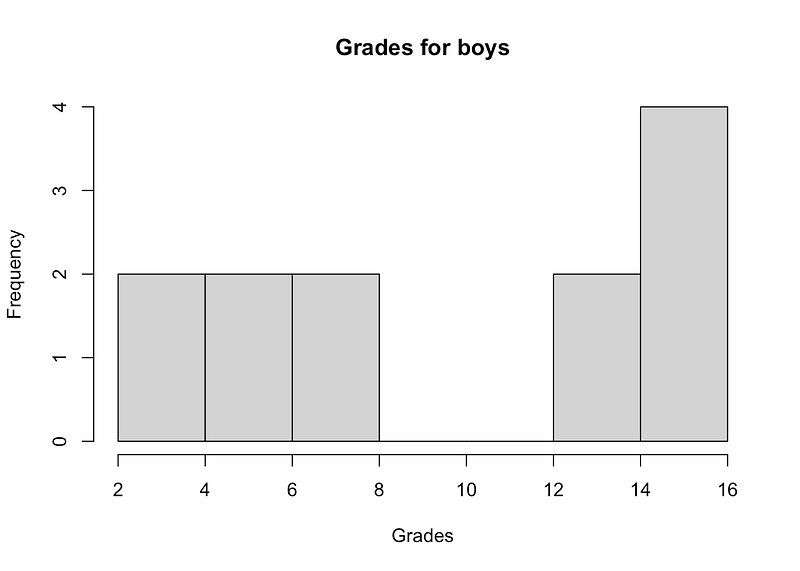
hist(subset(dat, Sex == "Boy")$Grade, main = "Grades for boys", xlab = "Grades")
The Shapiro-Wilk tests for normality yield:
shapiro.test(subset(dat, Sex == "Girl")$Grade)
shapiro.test(subset(dat, Sex == "Boy")$Grade)
Both histograms indicate that the distributions do not appear to follow a normal distribution, and the p-values from the Shapiro-Wilk tests confirm this conclusion (rejecting the null hypothesis of normality at the 5% significance level).
Since the normality assumption is violated for both groups, we can proceed to perform the Wilcoxon test in R. Remember that the null and alternative hypotheses for the Wilcoxon test are as follows:
- H0: The two groups are similar
- H1: The two groups are different
test <- wilcox.test(dat$Grade ~ dat$Sex)
The output will provide the test statistic, the p-value, and a reminder of the hypotheses tested.
The p-value obtained is 0.021. Thus, at the 5% significance level, we reject the null hypothesis, indicating that there is a significant difference in grades between girls and boys. The boxplot illustrates that girls seem to outperform boys, which can be formally tested by specifying the alternative = "less" argument in the wilcox.test() function:
test <- wilcox.test(dat$Grade ~ dat$Sex, alternative = "less")
The resulting p-value is 0.01, suggesting that, at the 5% significance level, we reject the null hypothesis and conclude that boys performed significantly worse than girls.
Paired Samples
For the second scenario, consider a situation where we administered a math test to a class of 12 students at the start of a semester, followed by a similar test at the end of the semester for the same students. The data collected is as follows:
dat <- data.frame(
Beginning = c(16, 5, 15, 2, 14, 15, 4, 7, 15, 6, 7, 14),
End = c(19, 18, 9, 17, 8, 7, 16, 19, 20, 9, 11, 18)
)
We will transform this dataset into a tidy format:
dat2 <- data.frame(
Time = c(rep("Before", 12), rep("After", 12)),
Grade = c(dat$Beginning, dat$End)
)
We can visualize the grade distributions at the beginning and after the semester using:
dat2$Time <- factor(dat2$Time, levels = c("Before", "After"))
ggplot(dat2) +
aes(x = Time, y = Grade) +
geom_boxplot(fill = "#0c4c8a") +
theme_minimal()
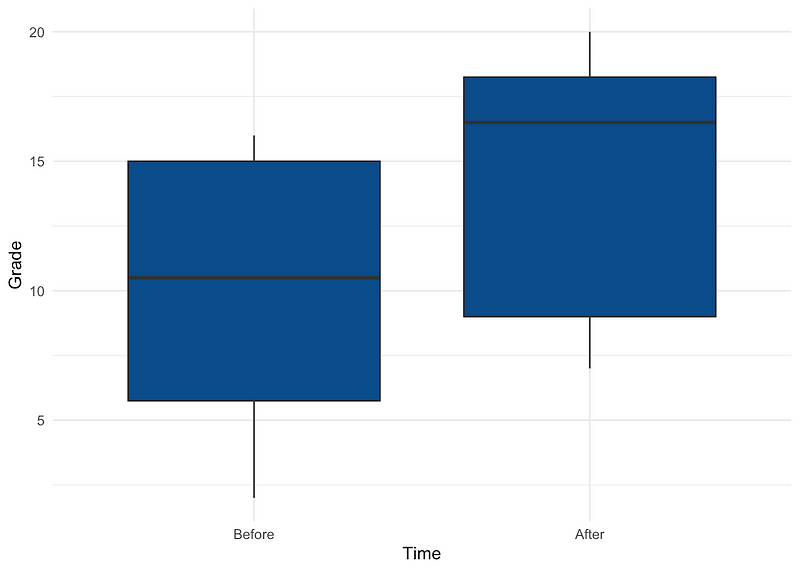
In this example, the two samples are clearly dependent since the same 12 students took the test before and after the semester. Assuming that the normality assumption is violated, we will utilize the Wilcoxon test for paired samples.
The R code for this test is similar to that for independent samples, with the addition of the paired = TRUE argument in the wilcox.test() function:
test <- wilcox.test(dat2$Grade ~ dat2$Time, paired = TRUE)
The output will yield the test statistic, the p-value, and a reminder of the hypotheses tested. The p-value is 0.169, indicating that we do not reject the null hypothesis at the 5% significance level, suggesting that the grades before and after the semester are not significantly different.
Assumptions of Equal Variances
As mentioned earlier, the Wilcoxon test does not require the assumption of normality. The necessity of equal variances may depend on your specific goal. If the aim is merely to compare the two groups, testing for equal variances is not mandatory, as the two distributions need not share the same shape. However, if your goal is to compare the medians of the two groups, ensuring that the distributions have the same shape (and hence, the same variance) becomes crucial.
Consequently, the results of your variance equality test will influence your interpretation: differences in the distributions or differences in the medians. In this discussion, we are focused on comparing the groups to ascertain distributional differences, which is why we have not tested for equality of variances.
This principle also applies when conducting the Kruskal-Wallis test to compare three or more groups (the non-parametric alternative to ANOVA): if the intent is simply to assess whether differences exist among the groups, homoscedasticity is not a requirement, while it must be satisfied for median comparisons.
Thank you for reading! I hope this article has clarified how to compare two groups that do not conform to a normal distribution in R using the Wilcoxon test. If you require the parametric version, refer to the Student’s t-test, and for comparing three or more groups, check out ANOVA.
As always, if you have any questions or suggestions related to this topic, feel free to leave a comment for the benefit of other readers.
Additional Resources
To test the normality assumption, consider using three complementary methods: (i) histogram, (ii) QQ-plot, and (iii) normality tests (with the Shapiro-Wilk test being the most common). For guidance on determining whether a distribution is normal, refer to our resources.
Keep in mind that to use the Student’s t-test (the parametric version of the Wilcoxon test), it is essential for both samples to follow a normal distribution. Therefore, even if one sample is normal while the other is not, the non-parametric test is generally recommended.
Note that the presence of ties (equal values) can hinder precise p-value calculations. This can be addressed by executing the exact or asymptotic Wilcoxon-Mann-Whitney test with adjustments for ties via the wilcox_test() function from the {coin} package.
We apply alternative = "less" (not alternative = "greater") because we are testing whether grades for boys are lower than those for girls, based on the dataset's reference level.
For a deeper exploration of the assumption of equal variances in the Wilcoxon test, check out the following articles: 1, 2 & 3.