# Two Fascinating Unresolved Issues in Number Theory
Written on
Chapter 1: Exploring Number Theory
Number theory, which delves into the properties and intricacies of whole numbers, has long captured the interest of not only mathematicians but also aspiring math students and enthusiasts alike. While significant progress has been made in this field, two particularly challenging problems remain unsolved. These mathematical conundrums continue to perplex scholars and provoke deep thought among even the most accomplished mathematicians.
Section 1.1: The Riemann Hypothesis
The first of these enduring challenges is the Riemann Hypothesis. This conjecture concerns the distribution of prime numbers and their interrelations. Specifically, it asserts that all nontrivial zeros of the Riemann zeta function, which represents the distribution of prime numbers, are found along the critical line of 1/2.
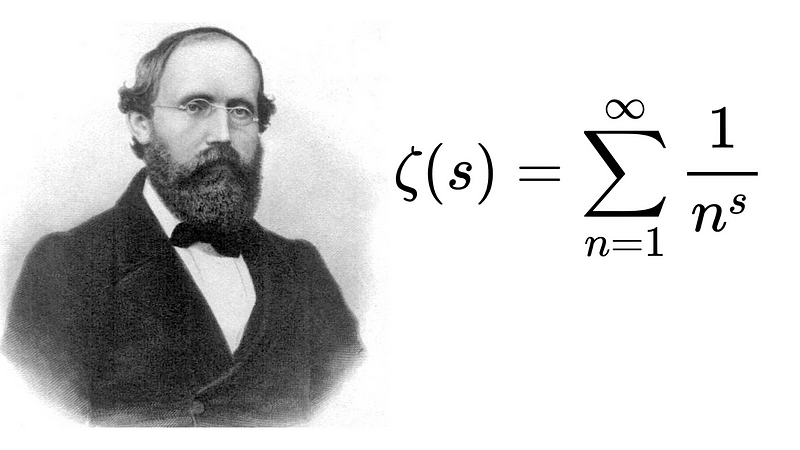
Bernhard Riemann first proposed this hypothesis in 1859 in a paper where he examined the distribution of prime numbers. In this work, he suggested that the nontrivial zeros of the Riemann zeta function had a specific location. Since then, the Riemann Hypothesis has attracted extensive research, with mathematicians globally attempting to either prove or disprove it. Despite numerous attempts, a definitive proof remains elusive. In 2000, the Clay Mathematics Institute designated the Riemann Hypothesis as one of the seven Millennium Prize Problems, offering a million-dollar prize for its resolution.
In this video titled "Top Ten Open Problems in Number Theory," you will get an overview of the most pressing issues in the field, including the Riemann Hypothesis.
Section 1.2: The Inverse Galois Problem
The second unresolved issue is the Inverse Galois Problem, which seeks to determine the conditions under which a Galois extension of the rational numbers exists with a specific Galois group. This question is a cornerstone of Galois theory, yet a general solution remains out of reach.

First posed in the mid-19th century, the Inverse Galois Problem continues to be a central open question in mathematics today. Despite extensive efforts from the mathematical community, its resolution is still pending. This problem fundamentally connects the dots between algebraic equations and their solutions, investigating what is necessary for a Galois extension of the field of rational numbers to exist with a specified Galois group. Over time, noteworthy advancements have been made, and the Inverse Galois Problem has spurred new research avenues and contributed to a broader understanding of mathematics and science.
Chapter 2: Implications Beyond Academia
These unresolved problems are not merely academic; they hold significant implications for various fields, including cryptography, where the distribution of prime numbers is vital for securing communication systems. The enduring nature of these challenges, despite the tireless efforts of mathematicians, underscores their complexity and highlights the richness inherent in number theory.
In the video "Hard Unsolved Math Problems," viewers can explore various difficult mathematical issues, including the Inverse Galois Problem.
Thank you for taking the time to read this exploration of number theory. If you found this content engaging, feel free to show your appreciation by hitting the clap icon as many times as you'd like. If you enjoy my work and wish to support it, consider becoming a Medium member through this link or buy me a coffee. Stay tuned for more intriguing stories!