Chapter 1: Introduction to Mathematical Induction

Mathematical induction is a powerful technique used to prove statements or formulas that are asserted to be true for all natural numbers. This method involves a series of logical steps, allowing mathematicians to establish the validity of these statements systematically.

To illustrate this principle, let's consider a specific formula that we want to validate using mathematical induction.

Step 1: Base Case (n = 1)

We begin by examining the base case:

• Left-Hand Side (L.H.S): (1^3 = 1)
• Right-Hand Side (R.H.S): ((1)^2 = 1)

Thus, we confirm that the formula holds true for (n = 1).

Step 2: Inductive Hypothesis

Next, we assume that the formula is valid for some arbitrary integer (n = k). This assumption will be vital for our inductive step.

Step 3: Inductive Step (n = k + 1)

Now, we proceed to prove the formula for (n = k + 1). We start with the left-hand side, where we denote the first (k) terms within brackets. Utilizing our hypothesis from Step 2, we reformulate the left-hand side:

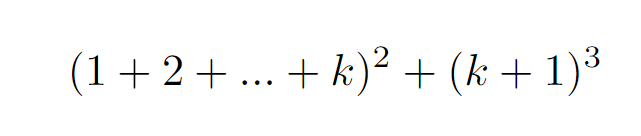
The key here is to apply the formula for the sum of the first (k) natural numbers to simplify our expression.

Step 4: Factorization

Next, we aim to factor our resulting expression.

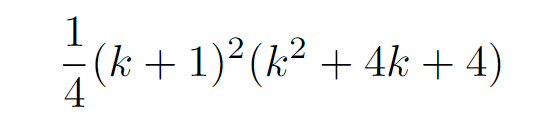
Notice that ( frac{1}{4} ) can be rewritten as ((frac{1}{2})^2), and we can further factor the quadratic expression to reveal a perfect square.

Step 5: Conclusion of Proof

Ultimately, we observe that our result simplifies to the square of the sum of the first (k + 1) natural numbers.

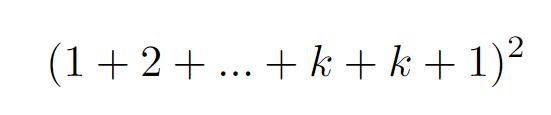
Thus, we have successfully demonstrated the validity of the formula through the principle of mathematical induction.

Further Learning

To deepen your understanding of mathematical induction, check out these helpful video resources:

The first video, "Mathematical Induction Practice Problems," offers various examples to solidify your grasp of the topic.

The second video, "How to do a Mathematical Induction Proof (Example 1)," presents a clear walkthrough of the proof process, enhancing your learning experience.

Conclusion

By following the structured steps of mathematical induction, we can effectively prove the validity of numerous mathematical formulas. If you found this guide helpful, feel free to share your thoughts or questions in the comments below.

Thank you for reading! If you enjoyed this content, consider supporting my work. Your encouragement means the world to me.