Understanding the Law of Sines: A Comprehensive Guide
Written on
Chapter 1: Introduction to Trigonometry
Trigonometry can be a daunting subject, particularly when it comes to memorizing its numerous formulas. But fear not! This guide is designed to simplify these concepts, starting from the basics for those who may be new to the field.
In geometry, figures typically possess two main characteristics: length and angle. Length refers to a segment that can represent a side of a polygon or the diameter of a circle, while angle measures the degree to which one line diverges from another. Early mathematicians sought to establish a connection between these two elements. However, since angles are only defined between two lines, a more logical relationship connects angles to the ratio of lengths between two segments. This relationship is encapsulated in the functions known as sine (sin) and cosine (cos).

To precisely define these relationships, sin and cos are established in the context of a right triangle.
It's important to note that angles ? and ? shown in the triangle are acute. However, as mathematics advanced, the definitions of sine and cosine expanded to include obtuse angles and even negative angles. For instance, for an obtuse angle x, we can express sin(x) as sin(180° - x) and cos(x) as -cos(180° - x). For the purposes of geometry, we won't delve into angles beyond 180° or negative angles.
For further insight into how algebra evolved from geometry, check out this informative video from Veritasium:
Chapter 2: The Law of Sines Explained
Let's dive deeper into the Law of Sines. Consider triangle ABC and its circumcircle ? with a radius R. Let O denote the center of ? and D a point on ? such that angle DBC equals 90°.

According to Theorem 1.12, angle BAC can be expressed as ½ angle BOC = angle BDC. Thus, we have the relationship sin(angle CAB) = sin(angle BDC) = BC/CD = BC/(2R). This leads us to the law of sines:

To derive this further, we define points E and F on ? such that angles ECA and FAB equal 90°. This leads us to the theorem:
Theorem 1.13
For any triangle ABC, the Law of Sines holds true.
When triangle ABC is a right triangle, the Law of Sines simplifies to the basic definition of sine. For example, when angle CAB is 90°, we find:
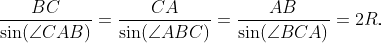
Next, let's explore an important property of the sine function. For any acute angle ?, sine is a monotonically increasing function: as ? increases, so does sin(?). The following illustration clarifies this concept.
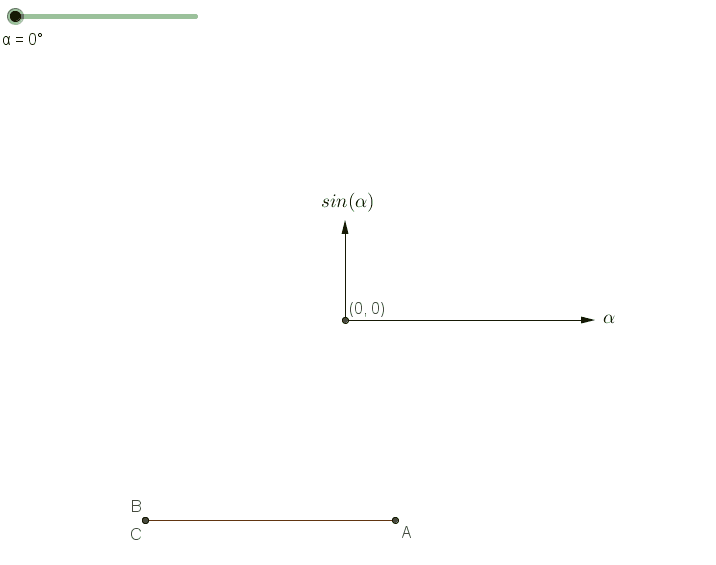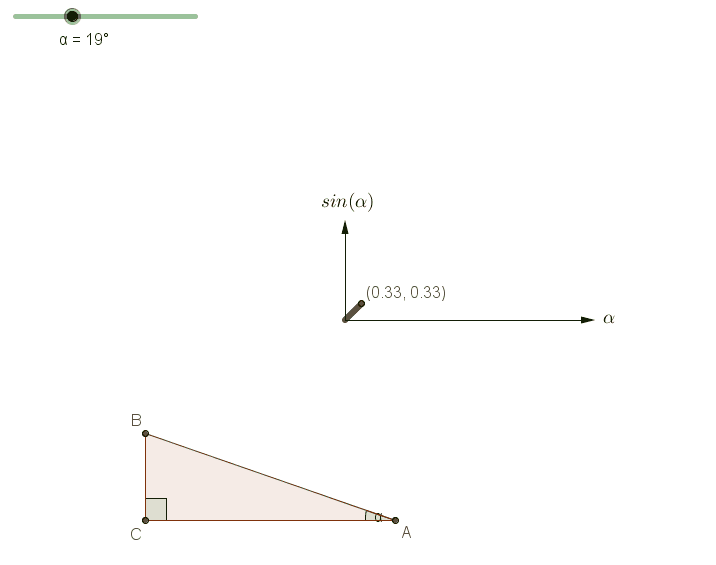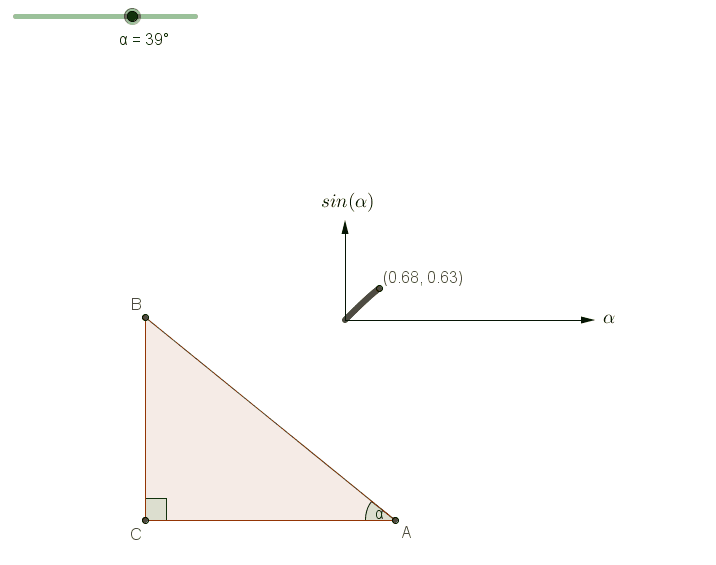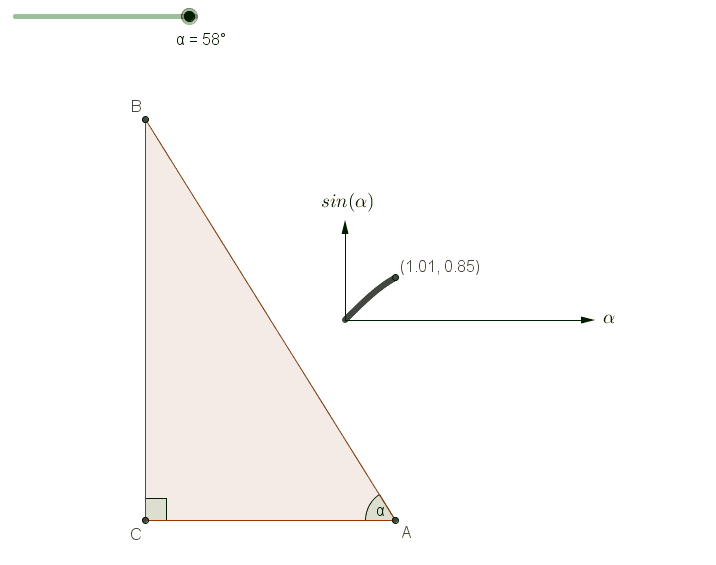
Assuming ABC is an acute triangle, we can infer from Theorem 1.13 and the increasing nature of the sine function that:
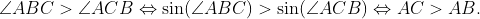
This reasoning extends to obtuse triangles as well. Without loss of generality, let's assume angle ABC is obtuse in triangle ABC. Then, 180° - angle ABC becomes an acute angle, and according to Theorem 1.3, we have 180° - angle ABC = angle ACB + angle BAC > angle ACB. Thus, we reach the conclusion that:

We can thus establish the following theorem:
Theorem 1.14
In any triangle ABC, angle ABC is greater than angle ACB if and only if side AC is greater than side AB.
This theorem illustrates the relationship between angles and the lengths of their opposite sides.
Endnote: In practice, I often resort to trigonometry only when simpler Euclidean methods fail to solve a problem. Some refer to this approach as "trigonometry bashing," among other analytical techniques. While using analytical geometry in competitions is permissible, I prefer to embrace the elegance of geometry itself.
Thank you for engaging with this content! If you found it valuable and wish to support my writing, consider joining as a member. For just $5 a month, you'll gain unlimited access to all my stories on Medium. Plus, signing up through my link will earn me a small commission.


