Exploring the Evenness of Products from 1 to 2024
Written on
Chapter 1: Understanding the Problem
The weather today has been quite unpredictable. It started off overcast in the morning, only to brighten up in the afternoon with the sun peeking through. As I write this at around 6:15 PM, the rain has returned in full force.
This brings us to an intriguing math puzzle involving the selection of two integers from a total of 2024! I encourage you to pause here, grab a pen and some paper, and give this a try. Once you’re ready, continue on for the solution!
Section 1.1: Analyzing the Product
When multiplying two integers, the result can either be even or odd. Our strategy will be to calculate the probability that the product is odd, and by subtracting that from one, we can find the probability of it being even.
The product of two integers is odd only when both integers are odd. For instance, (3)(5) = 15 is odd, while (4)(2) = 8 and (12)(5) = 60 are both even.
Considering the integers from 1 to 2024, there are 1012 odd integers (since 2024 divided by 2 equals 1012). Therefore, we can determine the probability of selecting two odd integers by calculating:
The resulting probability of the product being even can then be derived as follows:
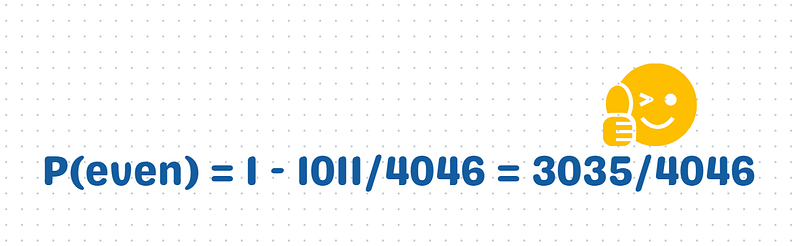
And there you have it—our answer!
Section 1.2: Extending the Analysis
What if we expand our findings to encompass the first n integers? How does the probability evolve as n approaches infinity?
Chapter 2: Share Your Thoughts
How fascinating is this problem? I’d love to hear about your thought process—please share your insights in the comments below!
If you enjoyed this, consider saving and sharing the list of the best math puzzles available on Medium.
Bella's Weekly Math Games
Join in on a 48-hour math competition every week!
If you want to be notified whenever I publish new content, be sure to sign up. Thank you for your support!
Thank you for taking the time to read this. If you found it valuable, please show your appreciation by clapping for the article.
If you enjoyed the article and would like to support my efforts, consider buying me a coffee! Your generosity is greatly appreciated and helps me continue my writing.
Happy Solving, Bella 😊