Chapter 1: Understanding Deep Neural Networks

The field of artificial intelligence (AI) has seen remarkable advancements thanks to deep neural networks (DNNs). However, one persistent challenge remains: determining the appropriate level of complexity for these networks. A DNN that lacks depth may fail to perform adequately, while one that is overly complex risks overfitting, leading to excessive computational demands.

In the recent publication, "Variational Inference for Infinitely Deep Neural Networks," researchers from Columbia University introduce an innovative model known as the unbounded depth neural network (UDN). This infinitely deep probabilistic model is designed to self-adjust to the training data, eliminating the need for deep learning experts to make difficult choices regarding the complexity of their DNN architectures.

The research team outlines their key contributions as follows: They introduce the UDN, which can generate data from any of its hidden layers and adapt its truncation in accordance with the observations in its posterior. They also propose a new variational inference technique featuring a unique variational family, which retains a finite yet adaptable set of variational parameters to navigate the unbounded posterior space of the UDN parameters. Their empirical analyses demonstrate that the UDN effectively adjusts its complexity based on the available data and surpasses the performance of both finite and infinite models.

Chapter 2: The Mechanics Behind UDN

The UDN consists of a DNN capable of arbitrary architecture and various layer types, along with a latent truncation level derived from a prior distribution. This setup allows the DNN to produce an infinite array of hidden states for each data point, utilizing these states to generate outputs. When provided with a dataset, the posterior UDN produces a conditional distribution over its weights and truncation depth, giving it the adaptability of an “infinite” neural network that can select the most suitable truncation distribution for the data.

The paper elaborates on a new method for approximating the UDN through variational inference, utilizing a "variational family" with an infinite number of parameters that encompasses the entire posterior space. Each member of this family supports a finite subset, allowing for efficient calculation and optimization of the variational objective. The team’s gradient-based algorithm facilitates the exploration of the infinite truncation and weight space, enabling the UDN to adjust its depth according to the complexity of the data.

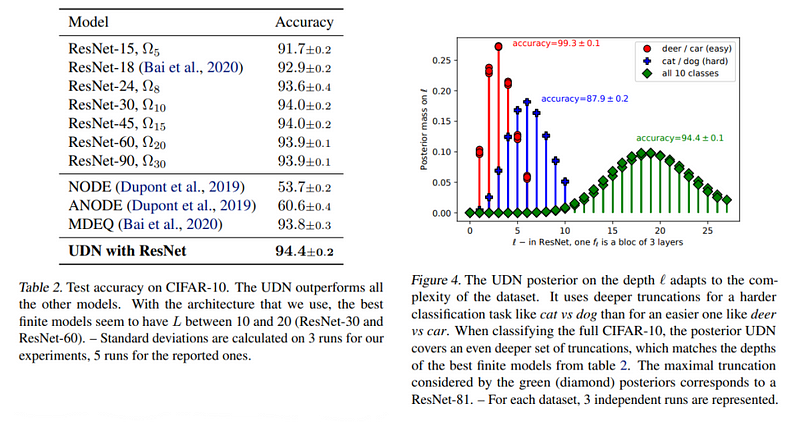
In their empirical evaluation, the researchers tested the UDN on both synthetic and real classification tasks. The model outperformed existing finite and infinite models, achieving 99% accuracy on simpler label pairs with just a few layers and 94% accuracy on the complete dataset. Moreover, the UDN showcased its capacity to modify its depth in response to data complexity, varying from a few layers to nearly one hundred in image classification tasks. The dynamic variational inference method also proved effective in exploring truncation spaces.

The authors anticipate that this research will pave the way for further investigations. Potential applications of the UDN include its use in transformer architectures, while the unbounded variational family may also assist in variational inference for other infinite models. Future studies could explore how the structure of the neural network’s weight priors influences the resulting posteriors.

The paper "Variational Inference for Infinitely Deep Neural Networks" is available on arXiv.

Stay updated with the latest news and breakthroughs in AI research by subscribing to our well-received newsletter, Synced Global AI Weekly, for weekly insights.