Changed Perspectives on Logic: The Impact of Two Pioneering Laws
Written on
Chapter 1: The Historical Context of Logic
The evolution of human logic is both extensive and fascinating. Historically, logic was intertwined with various fields of study, with renowned thinkers like Aristotle and Confucius heavily relying on fundamental logical principles in their discourse. The foundational ideas presented by these intellectual giants have endured well beyond their times. In Europe, the logical frameworks proposed by Aristotle remained largely unchallenged until the 17th century.
It was in the 1680s that Leibniz began to expand upon Aristotle's work, developing his version of symbolic logic, which he termed "the calculus of reason." However, his contributions went largely unnoticed until the 20th century due to their publication delays, leading to minimal immediate impact. Despite efforts from various scholars to advance beyond Aristotle's legacy, few succeeded.
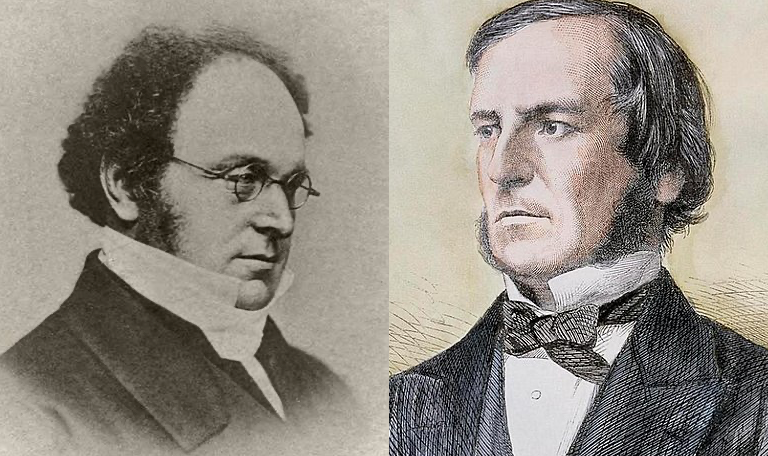
Chapter 2: The Emergence of Algebraic Logic
The landscape shifted dramatically in the 19th century with the arrival of George Boole, known for his work on Boolean variables, alongside August De Morgan and others. These figures established intricate systems of algebraic logic that gained substantial acceptance in both mathematical and philosophical circles.
Utilizing this novel logical framework, it became feasible to formally articulate many principles previously established by earlier scholars. De Morgan, in particular, contributed by formalizing what are now known as De Morgan’s Laws. While these two laws had earlier recognition from thinkers such as Aristotle and William of Ockham, De Morgan's algebraic approach rendered them rigorous and precise.
Section 2.1: Understanding De Morgan's Laws
In this discussion, I will introduce De Morgan’s laws through the lens of set theory to aid visualization, noting that their equivalents exist within formal logic. Let’s first clarify a few essential symbols.
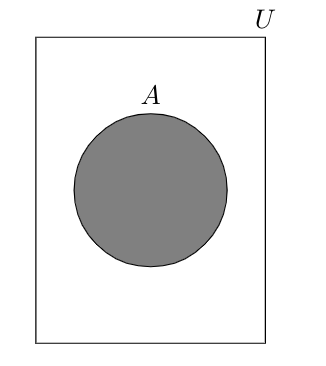
We define a set A as a collection of objects, where the specific elements are inconsequential for our discussion, only that A comprises certain items, all of which either belong to A or do not. These items also belong to U, the universal set containing all elements. As illustrated in Figure 1, some items in U are not part of A (highlighted in grey), but every item within A exists in U.
Section 2.2: Complement and Operations
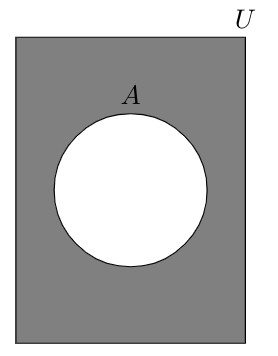
What about the elements not included in A? We denote this as A’, known as the complement of A, as shown in Figure 2 below.
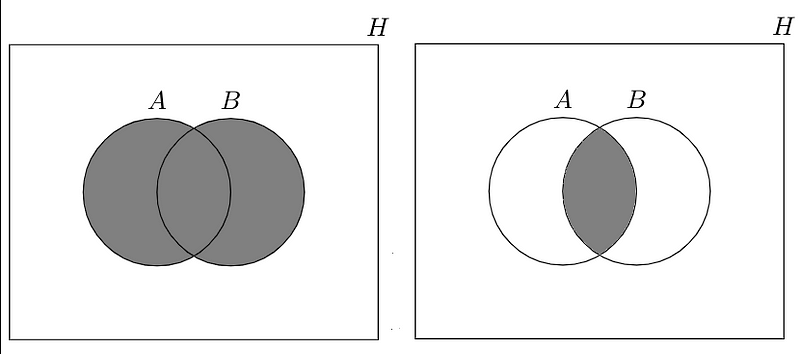
Only a few more symbols need clarification! If we consider two sets A and B, we can relate them through two operations: and (∩) and or (∪). To remember these definitions, envision how the symbol for "and" resembles a capital "A" with a missing middle line!
The expression A ∩ B refers to elements that are common to both sets (A and B), whereas A ∪ B encompasses all elements from A as well as all elements from B (A or B). This distinction may seem perplexing, so refer to Figure 3 for a clearer understanding!
Section 2.3: Formulating De Morgan’s Laws
Now, we can articulate De Morgan’s Laws, which are surprisingly straightforward:
- (A ∩ B)' = A' ∪ B'
- (A ∪ B)' = A' ∩ B'
Though these can be formally proven using set theory, I encourage you to sketch a diagram similar to those presented and deduce for yourself that both equalities hold true. Note that the use of the complement symbol (') signifies the complement of the set within the parentheses.
These laws are formal expressions of basic reasoning and signify a pivotal transition in logic towards symbolic representation. Both Boole and De Morgan played crucial roles in this transformation, shaping the contemporary landscape of logical theory. For a deeper exploration of the logical implications of these laws, I recommend reviewing this comprehensive resource. It also serves as an excellent primer for advanced mathematics and logical reasoning.
Thank you for taking the time to read! Feel free to share your thoughts or questions regarding this article. I hope you found it informative! If you appreciate my work, consider joining as a Medium member through this link to support my efforts! You can also follow me for more insights into math and science, as I publish weekly.